安全渣眼中的常见机器学习算法
0x01 前言
有好久没更新博客了,真的是有多少存货才能吐多少货,最近一段时间都在学习机器学习,想给网络安全插上机器学习的刺刀,本篇文章大多为理论,之后会更网络安全方面的机器学习应用。玩安全的人很多,玩机器学习的人也很多,但是这两者都玩的相对还是蛮少的。
0x02 常见的机器学习算法原理分析
常见的机器学习算法主要有:逻辑回归(LR)、支持向量机(SVM)、K-近邻(KNN)、朴素贝叶斯(NB)、决策树(DT)、随机森林(RF)、K均值(K-means)、马尔可夫、Adaboost、神经网络
一篇文章无法详细解释以上这十种常见算法,本来是想直接把手稿贴上来完事的,毕竟手稿才原汁原味,写出来难免失真,后来想想还是得总结一下写出来,都说多一个数学公式会少一半读者,但是公式是最直接的,想到哪写到哪吧,公式纯手打,如有错误请跳过。
1.逻辑回归算法
(1)参考阅读:https://zhuanlan.zhihu.com/p/28775274
http://www.csuldw.com/2016/09/19/2016-09-19-logistic-regression-theory/
http://blog.csdn.net/zouxy09/article/details/20319673
http://blog.csdn.net/han_xiaoyang/article/details/49123419
(2)知识点:sigmoid函数、梯度下降法进行最优值求解
(3)算法推导:
(4)难点:为什么要用sigmoid函数?这涉及到Ng公开课中提到的Exponential family,即指数族,具体的推导可以参考https://www.zhihu.com/question/35322351
(5)总结:逻辑回归将原本输出结果范围可以非常大的θTX 通过sigmoid函数映射到(0,1),从而完成概率的估测。求解逻辑回归参数的传统方法是梯度下降,构造为凸函数的代价函数后,每次沿着偏导方向(下降速度最快方向)迈进一小部分,直至N次迭代后到达最低点
2.SVM
(1)参考阅读:https://www.zhihu.com/question/21094489
http://www.hanlongfei.com/convex/2015/11/08/kkt/
http://blog.csdn.net/v_july_v/article/details/7624837
http://blog.sina.com.cn/s/blog_4298002e010144k8.html
(2)知识点:函数间隔、几何间隔、最优间隔分类器、KKT条件、对偶问题、kernel
(3)算法推导: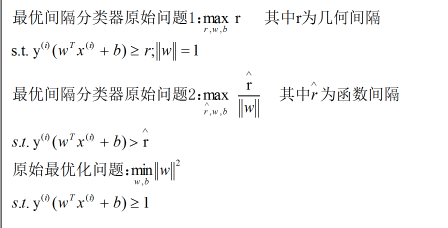
为什么进行原始问题转化,因为原始问题1中的约束为非凸性约束,原始问题2中的目标为非凸性优化目标,都不利于优化,这涉及到数学中的凸优化问题,可以参考http://www.zhihu.com/question/20343349。原始问题1转化为原始问题2,主要利用函数间隔和几何间隔的关系;原始问题2转化为原始最优问题,主要是令函数间隔为1。为什么可以令为1,是因为可以成倍调整w和b,几何间隔不变,而函数间隔变化,也即是可以取值令函数间隔取为1。接下来进行原始最优问题的求解,这涉及到KKT条件和对偶问题的转化。
原始最优化问题利用拉格朗日乘子法可以化为(1)式

以上的SVM只能处理线性的情况,但是在得到对偶问题形式后,再通过Kernel推广到非线性的情况就很容易了。关于Kernel请自行深入
(4)难点:如何理解低维空间线性不可分通过映射到高维空间实现线性可分?
(5)总结:使用Kernel可以解决非线性的分类
3.朴素贝叶斯
(1)参考阅读:https://yq.aliyun.com/articles/113512?t=t1
https://zhuanlan.zhihu.com/p/25493221
http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html
(2)知识点:主要是概率论基础,包括但不限于:贝叶斯定理、全概率公式
(3)算法推导:
(4)难点:主要是概率论的知识忘完了
(5)总结:所谓的朴素贝叶斯,“朴素”代表的是特征条件独立,“贝叶斯”代表的是基于贝叶斯定理。其实就是用先验概率来得到每一类的分类后验概率,取最大值作为其分类。
4.决策树
(1)参考阅读:https://www.ibm.com/developerworks/cn/analytics/library/ba-1507-decisiontree-algorithm/index.html
http://www.cnblogs.com/pinard/p/6050306.html
http://blog.csdn.net/u010161630/article/details/51699553
(2)知识点:熵、条件熵、联合熵、信息增益、信息增益率、基尼系数
(3)算法推导:决策树分类算法流程为:选取特征、决策树生成、决策树剪枝。典型的算法为ID3、C4.5、CART三种。其中ID3算法是用信息增益的大小来判断当前节点应该选取什么特征来构建决策树;C4.5算法是用信息增益率来作为选取特征的标准;CART算法是用基尼系数来作为选取特征的标准。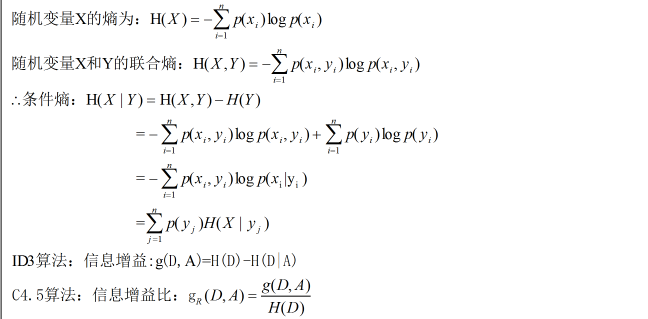
(4)难点:ID3算法的缺点和C4.5算法相对于ID3的改进的理解,见总结
(5)总结:互信息是指两个随机变量间的关联程度,ID3决策树中的信息增益等价于训练集中类与特征的互信息,信息增益表示由于特征A而使数据集D的分类的不确定性减少的程度,信息增益大的特征具有更强的分类能力。其中ID3算法主要有四个缺点:1、不能处理连续特征;2、用信息增益作为标准容易偏向于取值较多的特征;3、没有考虑缺省值;4、没有考虑过拟合。所以C4.5算法依次改进了ID3的四个缺点:1、将连续的特征离散化;2、用信息增益比作为标准;3、缺省值问题详细参考http://www.cnblogs.com/pinard/p/6050306.html;4、引入正则化系数进行初步剪枝
5.随机森林
(1)参考阅读:https://zhuanlan.zhihu.com/p/21358126
https://zhuanlan.zhihu.com/p/22097796
https://www.zhihu.com/question/30295075
https://www.zhihu.com/question/26898675
(2)知识点:采样、完全分裂
(3)算法描述:构造随机森林的过程有两个方面:数据的随机性选取、待选特征的随机选取(内含决策树算法)
a、数据的随机性选取:从原始的数据集中采用有放回的抽样,构造子数据集,且子数据集的数据量和原始数据数据量相同。比如有N个样本,则有放回的抽取N个样本作为子数据集。该子数据集用来训练一个决策树,作为决策树跟节点处的样本。
b、候选特征的随机选取:从所有的候选特征中随机选取一定的候选特征,再在随机选取的特征中选取最优的特征作为分裂特征(联系ID3,C4.5,CART的分裂特征选取标准),进行完全分裂。比如每个样本有M个属性,在决策树的每个节点需要分裂时,随机从M个属性中随机选取m个属性,且m远小于M,然后从这m个属性中采用某种策略(ID3是信息增益、C4.5是信息增益比)选取1个属性作为该节点的分裂属性。决策树形成过程中每个节点都按照上述步骤来分裂,直到完全分裂,建立出决策树。
(4)难点:为什么随机森林不易出现过拟合?因为样本和特征都是随机选取的,比如,生成的每个决策树实际上用到的样本只是原始样本的一部分,所以不易过拟合。
(5)总结:决策树是一种单一分类器。而随机森林是一种组合分类器。组合分类器比单一分类器分类效果好,比如ID3决策树易过拟合,而随机森林不易。随机森林是一种利用多个分类树对数据进行分类和判断的方法,在对数据进行分类的同时,还可以给出各个节点变量(feature即特征)的重要性评分,评估各个变量在分类中所起的作用
6.KNN
(1)参考阅读:http://www.saedsayad.com/k_nearest_neighbors.htm
https://zhuanlan.zhihu.com/p/22345658?utm_source=tuicool&utm_medium=referral
(2)知识点:欧式距离、归一化
(3)算法描述: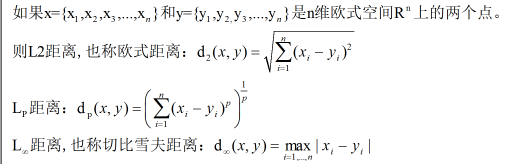
knn算法是指一个样本在特征空间中距离最近的k个样本点中大多数属于某一个类别,那么该样本也属于这个类别。而其中提到的距离一般是指欧式距离,即L2距离。
(4)难点:计算距离的时候需要考虑特征归一化的问题。因为需要考虑到特征的权重,比如一个特征的数据数值远远大于另一个特征的数据数值(但这两个特征都很重要),那么前一个特征将会起到决定性作用,这是要避免的,这就要进行归一化的操作,把大数据值进行归一化,避免失衡。
(5)总结:KNN算法比较简单,便于理解,但是计算量大,因此用处不是很大
7.K-means
(1)参考阅读:http://wepon.me/2015/08/20/KMeans/
http://www.datasciencelab.cn/clustering/kmeans
https://yq.aliyun.com/ziliao/topic_219
(2)知识点:无监督学习、聚类
(3)算法描述:
(4)难点:a、在算法描述2中,K-means如果保证所谓的收敛?b、K-means与EM的关系(K-means中蕴含的EM思想)。K-means核心点,包括这两个我觉得难的点都在http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006910.html中可以找到
(5)总结:K-means算法的优势在于性能和聚类效果,同时它也存在一些局限。第一个是不能发现非凸形状的簇;第二个是它的收敛是到局部最优而不是全局最优,收敛的结果很大程度上取决于初始质心点的选取,但可以被选择多组初始值重复使用K-means算法计算后取最优来缓解。
10/12更新 未完待续 还差 马尔可夫